現在位置が特定の範囲内か範囲外か調べたい
こんちか!!たくみんです。今日は、業務で使用した「ある点が特定の範囲(多角形)の内側か外側かを判定する機能」を実現するアルゴリズムとその実装について紹介します。
1. Crossing Number Algorithm
1-1. 概要
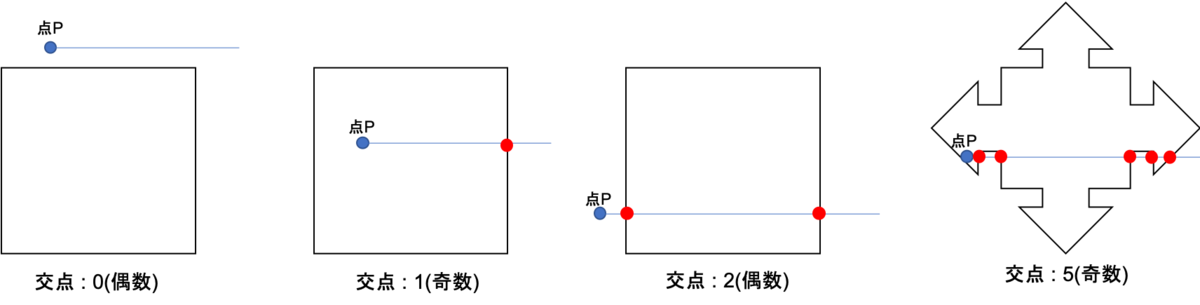
Crossing Number Algorithmは、ある点Pの右側から伸びる水平線と多角形の辺の交点の個数によって内側、外側を判定するアルゴリズムです。下図をみても分かる通り、偶数および0の場合は「外側」、奇数の場合は「内側」と判定します。
1-2. 自己交差している多角形に対する判定
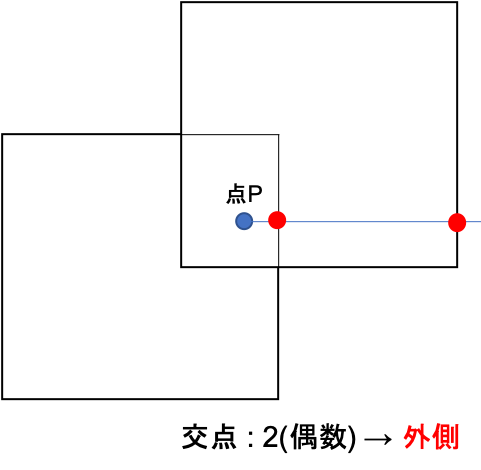
このアルゴリズムは、下図のように自己交差している多角形に対し、うまく判定してくれません。点Pが多角形の内側にあるにも関わらず、交点の数が偶数となってしまうため、外側と判定されてしまいます。自己交差している多角形に対してもうまく判定してくれるアルゴリズムにWinding Number Algorithmがありますが、今回は割愛します。
1-3. 点が多角形の辺上に存在する場合
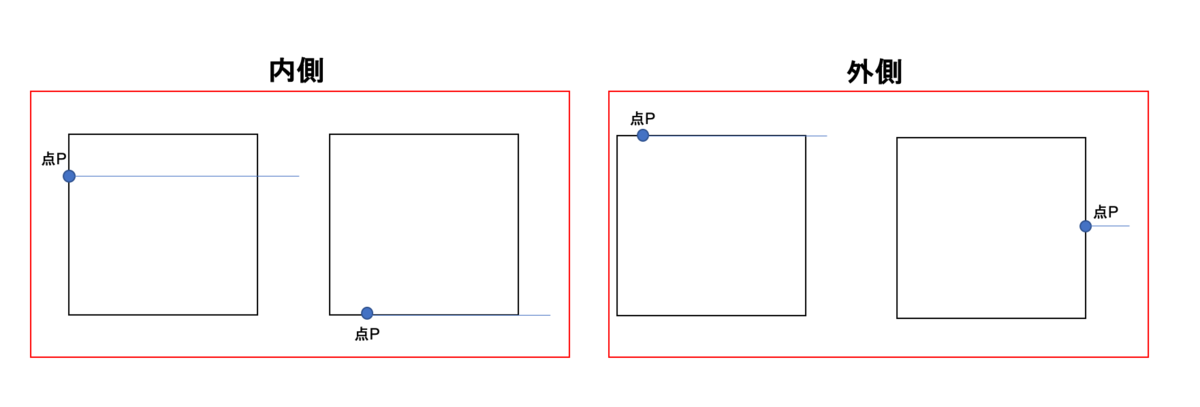
点が多角形の辺上に存在する場合人、内側とするか外側とするかを決めないといけません。一般的に左および下の辺にある場合は内側、右および上の辺にある場合は外側と判定するようです。
1-4. 判定方法
以上のことを踏まえると、以下のルールにより正しく判定することができます。
- 下向きの辺は開始点を含まず、終点を含む
- 上向きの辺は開始点を含め、終点を含まない
- 水平となる辺は判定対象としない
- 点Pの水平線と辺の交点は点pの右側にあること
2. 直線の方程式
点Pからのビル水平線と辺の交点のX座標を求めるために直線の方程式を使用します。
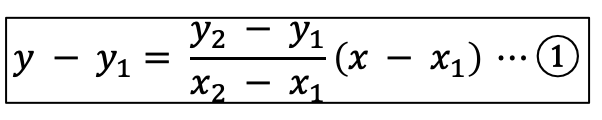
例として、以下の図で考えてみます。
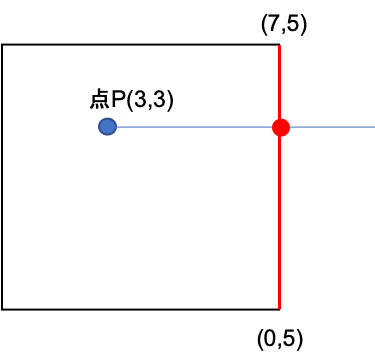
交点のX座標を求めるために、①の式をXについて解きます。
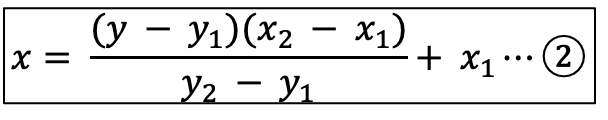
次に、図をもとに②の式に以下を代入します。
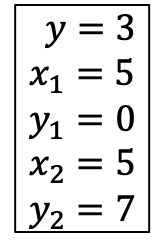

よって、点Pから伸びる水平線と辺の交点のX座標は5であると求めることができました。Crossing Number Algorithmでは、ここで求めたX座標が点PのX座標より大きいか判定します。今回の場合だと求めたX座標が点PのX座標よりも大きいため、辺が点Pよりも右側にあると判定します。これを多角形を構成する全ての辺に対して行い、右側に存在する辺の個数が奇数であれば範囲内、偶数であれば範囲外とします。
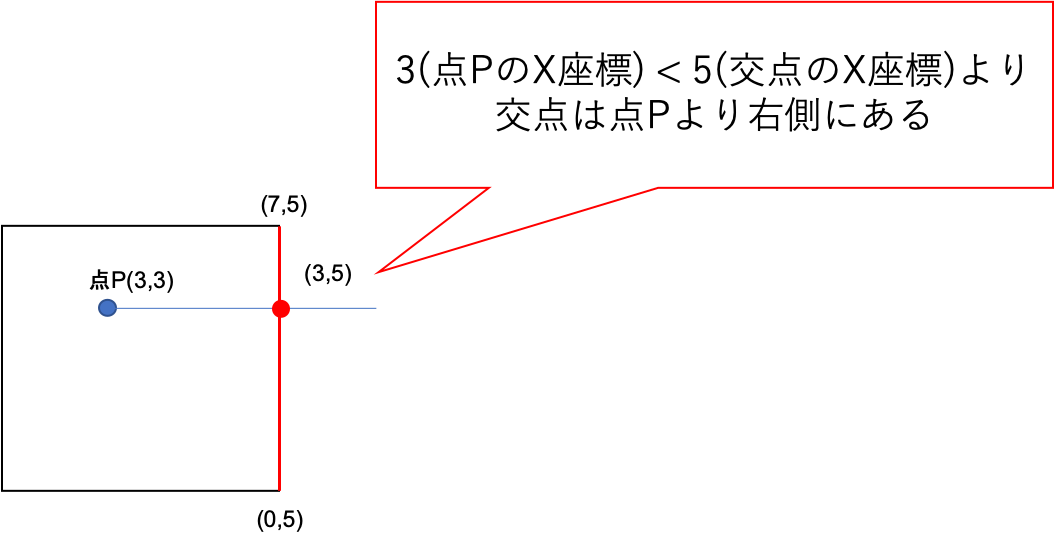
3. 実装
以上の点を踏まえて、プログラムの実装を行います。最近仕事でAngularを使い始めたのでAngularで実装してみます。
3-1. バージョン
- Angular 9.1.6
- Angular CLI 9.1.5
- Node 13.11.0
3-2. ディレクトリ構成(appディレクトリ下)
componentはCanvasComponentとTopPageComponentの2つで、サービスクラスはCrossingNumberAlgorithmServiceの1つです。
.
├── app-routing.module.ts
├── app.component.css
├── app.component.html
├── app.component.spec.ts
├── app.component.ts
├── app.module.ts
├── compoents
│ ├── Canvas // 点や図形を表示するcanvasを定義したcomponent
│ │ ├── Canvas.component.css
│ │ ├── Canvas.component.html
│ │ ├── Canvas.component.spec.ts
│ │ └── Canvas.component.ts
│ └── TopPage // CanvasComponentを表示するページのcomponent
│ ├── TopPage.component.css
│ ├── TopPage.component.html
│ ├── TopPage.component.spec.ts
│ └── TopPage.component.ts
└── service
├── CrossingNumberAlgorithm.service.spec.ts
└── CrossingNumberAlgorithm.service.ts // アルゴリズムのロジック
3-3. TopPageComponent
3-3-1. HTML
CSSフレームワークとしてBulmaを使用しています。
CanvasComponentを子コンポーネントとして呼び出しているだけです。
<nav class="navbar is-dark" role="navigation" aria-label="main navigation"> </nav> <app-Canvas></app-Canvas>
3-4. CanvasComponent
3-4-1. HTML
canvasタグにテンプレート参照変数と、クリックイベントを指定してます。 テンプレート参照変数を指定することで、canvasをTS側で参照できるようにします。 また、クリックイベントによりクリックした座標に点を配置するようにします。
<section> <div class="canvas"> <canvas #crossingNumberAlgorithmCanvas (click)="onClickCanvas($event)" width="600" height="600"> </canvas> </div> </section>
3-4-2. CSS
CSSはただセンタリングしているだけです。
.canvas { text-align: center; padding: 20px; } .canvas canvas { border: 1px #000 solid; width: 600px; height: 600px; }
3-4-3. TS
@ViewChildはcomponentを描画した後に要素を取得するため、ngInit()ではなく、ngAfterViewInit()を使用します。
ngAfterViewInit()では、範囲判定の対象となる図形の表示を行います。図形の座標は、CrossingNumberAlgorithmService内で定義しています。
import { Component, OnInit, AfterViewInit, ViewChild } from '@angular/core'; import { CrossingNumberAlgorithmService } from 'src/app/service/CrossingNumberAlgorithm.service'; @Component({ selector: 'app-Canvas', templateUrl: './Canvas.component.html', styleUrls: ['./Canvas.component.css'] }) export class CanvasComponent implements OnInit, AfterViewInit { /** canvasタグを特定する用 */ @ViewChild('crossingNumberAlgorithmCanvas') crossingNumberAlgorithmCanvas; /** canvasタグ用 */ public canvas: HTMLCanvasElement; public ctx: CanvasRenderingContext2D; /** 範囲判定を行う図形は固定 */ public lines = this.crossingNumberAlgorithmService.LINES; constructor(private crossingNumberAlgorithmService: CrossingNumberAlgorithmService) { } ngOnInit() { } /** viewChildが描画語でなければ参照できないいため使用 */ ngAfterViewInit() { this.canvas = this.crossingNumberAlgorithmCanvas.nativeElement; this.ctx = this.canvas.getContext( '2d' ); // 指定した座標に沿って線を引く for (let i = 0; i < this.lines.length - 1; i++) { this.ctx.beginPath(); this.ctx.moveTo(this.lines[i].x, this.lines[i].y); this.ctx.lineTo(this.lines[i+1].x, this.lines[i+1].y); this.ctx.closePath(); this.ctx.stroke(); } } /** * canvas内をクリック時 * クリックした箇所に点をうつ * 範囲内であれば赤点、範囲外であれば青点とする * @param event */ onClickCanvas(event) { // canvasの左上を(0,0)とするために座標計算 let rect = event.currentTarget.getBoundingClientRect(); let x = event.x - rect.left; let y = event.y - rect.top; // 点をうつ this.drawPoint(x, y); } /** * 引数として与えられた座標に点をうつ * 範囲内であれば赤点、範囲外であれば青点とする * @param x * @param y */ drawPoint(x: number, y: number) { // 点をうつ this.ctx.beginPath(); this.ctx.arc( x, y, 1, 0, Math.PI*2, false ) ; // 範囲内: Styleを赤, 範囲外: Styleを青 this.crossingNumberAlgorithmService.checkWithInPoint(x, y)? this.ctx.strokeStyle = "red" : this.ctx.strokeStyle = "blue" ; this.ctx.lineWidth = 1 ; this.ctx.stroke(); } }
3-5. CrossingNumberAlgorithmService
checkWithInPoint()内で CrossnigNumberAlgorithmを実装しています。
import { Injectable } from '@angular/core'; @Injectable({ providedIn: 'root' }) export class CrossingNumberAlgorithmService { /** 範囲判定を行う図形(図形を構成する点の座標を配列として表す) */ public LINES:{x: number, y: number}[] = [ { x: 100, y: 100, }, { x: 150, y: 150, }, { x: 200, y: 150, }, { x: 300, y: 200, }, { x: 300, y: 50, }, { x: 400, y: 50, }, { x: 450, y: 200, }, { x: 500, y: 200, }, { x: 500, y: 300, }, { x: 350, y: 500, }, { x: 350, y: 300, }, { x: 200, y: 400, }, { x: 200, y: 500, }, { x: 100, y: 300, }, { x: 100, y: 100, }, ] constructor() { } /** * 引数として渡された点が範囲内であるか判定する * @param pointX * @param pointY * @return true: 範囲内, false: 範囲外 */ checkWithInPoint(pointX: number, pointY: number): boolean { let withIncount: number = 0; for (let i = 0; i < this.LINES.length - 1; i++) { // 点のY座標が辺の始点と終点の間に存在するか(上向きの辺の場合) if( ((this.LINES[i].y <= pointY) && (this.LINES[i + 1].y > pointY)) // 点のY座標が辺の始点と終点の間に存在するか(下向きの辺の場合) // このif文<figure class="figure-image figure-image-fotolife" title="実装結果">[f:id:takuminv:20200523162720g:plain]<figcaption>実装結果</figcaption></figure>により点の水平線(右側のみ)と交わることのない辺を除去 || ((this.LINES[i].y > pointY) && (this.LINES[i + 1].y <= pointY))) { // 直線の方程式より、点の水平線(右側のみ)と辺の交点のX座標を求める let dx = (pointY - this.LINES[i]. y) * (this.LINES[i + 1].x - this.LINES[i].x) / (this.LINES[i + 1].y - this.LINES[i].y) + this.LINES[i].x; if (pointX < dx) { withIncount++; } } } // 奇数: 範囲内, 偶数: 範囲外 return withIncount % 2 !== 0 ? true : false; } }
4. 実装結果
ちょっと見えずらいですが、図形の範囲内の時は赤点、範囲外の時は青点になっていることがわかります。

5. おわりに
このようにcanvasを使用したことで判定が正しくできていることが目に見えてわかるため、実装してよかったと思います。ではでは。
6. おまけ
点をcavas内の全ての座標に配置するようにしたら次のようになりました。きれい。

7. 参考にしたサイト
SSの通知は高海千歌ちゃんにしてほしい
はじめに
こんちか!!たくみんです。これは、ラブライブ アドベントカレンダー 24日目(実質初日)の記事です。ほんとは18日にしていたんですけど、時間がなくて記事が書けなかったので24日に移動しました。 adventar.org
この記事では、僕が一番最初に作成したAqours SlackBotのSS通知 高海千歌BOTを紹介します。
SSとは
SS(Short Story)とはいわゆる2次創作の小説のようなものです。
なぜ作ろうと思ったのか
僕はラブライブのSSを読むのが日課になっており、ひどい時には1日中SSをあさっては読むということを繰り返していました。そうなると「新しいSSまとめられてるかな?」→「まだ出てない」→10分後 →「出てるかな」→「出てない」ということが多くなりました。いちいちサイトを確認して更新されているかどうかを確認するのは少々めんどくさいので更新されているかどうか通知する何かを作ればいいのではないかと思うようになりました。そこで、せっかくラブライブのSSを通知するのであればAqoursのキャラのBOTを作ればいいのでは???と思い開発することにしました。
通知する内容
通知する内容は、以下のサイトの内容です。
このサイトの赤ワクで囲まれたタイトル(URL)と登場人物などの箇所を取得します。
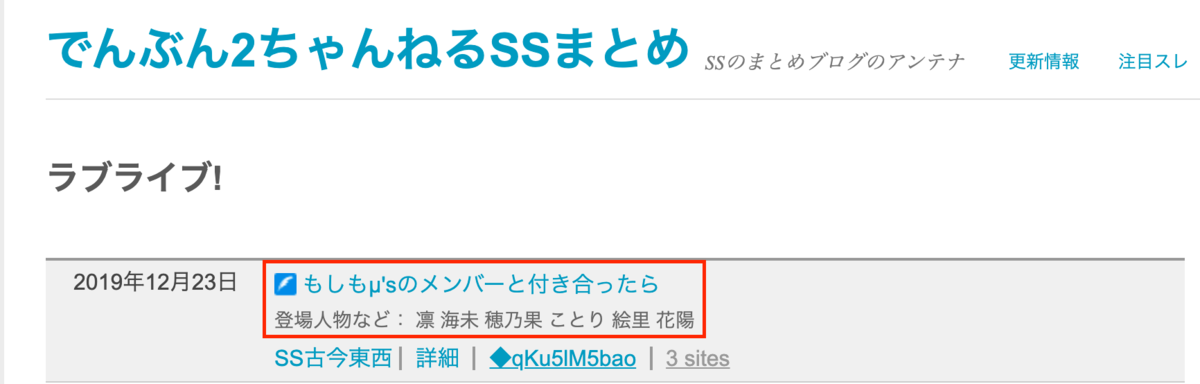
ソースコード
Model
Modelは以下の3つになります。タイトルとURLを管理するShortstory、登場人物等のTagを管理するTag、それらの中間テーブルのShortstoryTagの3つです。以前は私のお気に入りの別サイトからSSの情報を取得していました。その時はSS:Tag=1:多の関係だったのでわざわざ中間テーブルを設けています。現在 scrapingしているサイトはTagが1つになってしまったので意味のない中間テーブルになっています(また別サイトから取得することになった時のために残している)。
Shortstory
class Shortstory < ApplicationRecord has_many :shortstory_tag has_many :tag, through: :shortstory_tag accepts_nested_attributes_for :shortstory_tag, allow_destroy: true validates :title, presence: true validates :url, presence: true, uniqueness: true end
ShortstoryTag
class ShortstoryTag < ApplicationRecord belongs_to :shortstory belongs_to :tag end
Tag
class Tag < ApplicationRecord has_many :shortstory_tag has_many :shortstory, through: :shortstory_tag accepts_nested_attributes_for :shortstory_tag validates :name, presence: true, uniqueness: true end
rakeTask
このSSBotはRailsのrakeタスクを用いています。DBへの登録などはRailsにお任せしています。
# coding: utf-8 require 'http' require 'json' require 'uri' require 'dotenv' namespace :shortstory do desc "ss_set" task :ss_set => :environment do # SS情報を取得 new_ss_count = 0 Dotenv.load doc = ss_scraping(ENV["NOKOGIRI_URL"]) p doc p ENV["NOKOGIRI_URL"] 15.times do |k| ss_title = doc.css(".title")[k].children[1].children[1].text ss_url = doc.css(".title")[k].children[1].children[1]["href"] ss = Shortstory.new(title: ss_title, url: ss_url) tag = doc.css(".words")[k].text ss_tag = Tag.new(name: tag) # SS情報をDBに登録 if ss_tag.save ss.tag << ss_tag else ss.tag << Tag.find_by(name: tag) end if ss.save # 最初だけセリフ付き if (new_ss_count == 0) slack_post_text(ENV["SLACK_POST_URL"]) new_ss_count += 1 end # SlackにPOST slack_post(ss,ENV["SLACK_POST_URL"]) end end end end # SS情報を取得 def ss_scraping(url) charset = nil html = open(url) do |f| charset = f.charset f.read end doc = Nokogiri::HTML.parse(html, nil, charset) return doc end # SlackにPOST def slack_post(ss,url) uri = URI.parse(url) fields = [] ss.tag.each_with_index do |t,k| fields[k] = {:title=>t.name} end payload = { attachments: [ { title: ss.title, title_link: ss.url, fields: fields, color: "#36a64f" } ] } Net::HTTP.post_form(uri, { payload: payload.to_json }) end # セリフを言う def slack_post_text(url) uri = URI.parse(url) payload = { text: "<@XXXX> ssが更新されたよ~" } Net::HTTP.post_form(uri, { payload: payload.to_json }) end
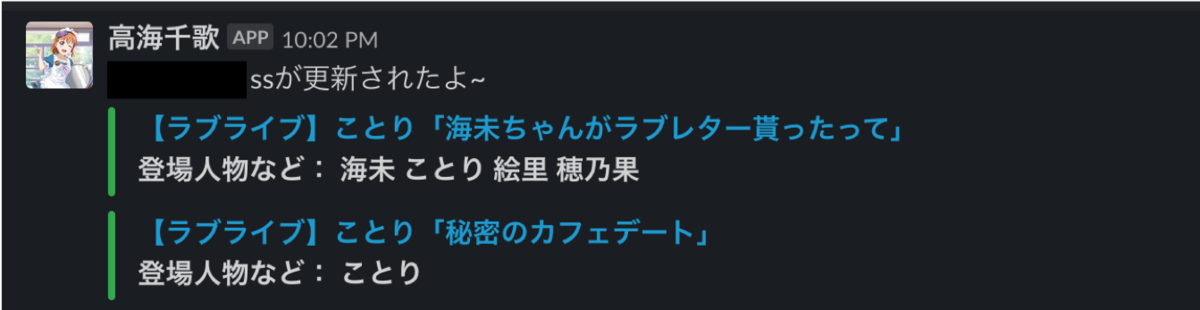
完成したもの
完成したSSBotです。これで安心してSSを読むことができますね。
おわりに
いつ記事にしようか迷っていたものを記事にできてよかったです。これからもラブライブに関連する何かを作れたらいいなと思います。ではでは。
PS Aqours総SlackBot化計画
僕の野望としてAqours総SlackBot化計画があります。これは「Aqours9人のBotを開発することで実質9人と一緒にいるのと同じではないか」という野望です。今現在、高海千歌Botを含め、3人のBotを開発しています。
桜内梨子Bot
黒澤ダイヤBot
9人全員のBotを作るのはいつになるのか。
Spring Bootでログイン画面を作る
こんちか!!たくみんです!!最近、会社でSpring Frameworkを使っているので「Spring Bootの勉強してみっか!」ということで勉強しています。そして簡単なログイン画面の実装に4時間を費やしたので備忘録としてこの記事を書きます。
目次
- 目次
- Spring Security
- ログイン画面
- LoginControllerクラス
- Employeeクラス(Entitiy)
- EmployeeRepositoryクラス
- LoginServiceクラス
- WebSecurityConfigクラス
- デモ
- まとめ
- 参考にしたサイト
Spring Security
ログイン画面
ログイン画面です。ただログインIDとパスワードを入力するだけの画面です。
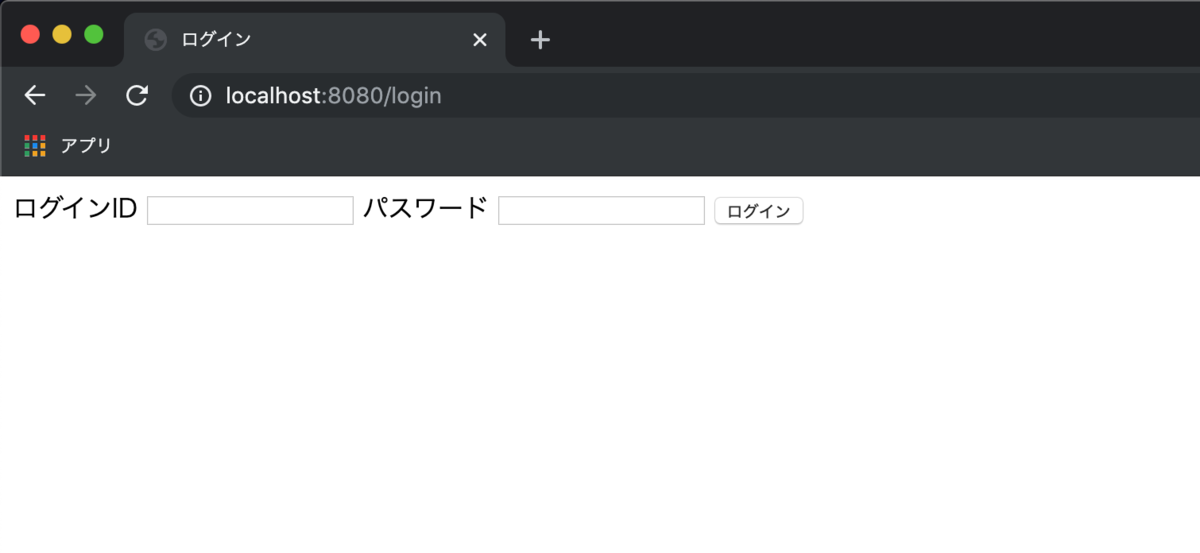
<!DOCTYPE html> <html xmlns:th="http://www.thymeleaf.org"> <head> <meta charset="UTF-8"> <title>Title</title> </head> <body> <form th:method="POST" th:action="@{/login}"> <label for="loginId">ログインID</label> <input type="text" name="loginId" /> <label for="passWord">パスワード</label> <input type="password" name="passWord" /> <input type="submit" value="ログイン" /> </form> </body> </html>
LoginControllerクラス
ログイン画面のControllerクラスです。このContollerでは/loginのGETリクエストに対して、ログイン画面を表示するようにしているだけです。
package com.example.demo.app.controller; import org.springframework.stereotype.Controller; import org.springframework.web.bind.annotation.GetMapping; import org.springframework.web.bind.annotation.RequestMapping; import org.springframework.web.servlet.ModelAndView; @Controller @RequestMapping("login") public class LoginController { @GetMapping public ModelAndView index(ModelAndView modelAndView) { modelAndView.setViewName("/login/index"); return modelAndView; } }
Employeeクラス(Entitiy)
今回は従業員管理システムという想定でログイン画面を作りました。このEmployeeクラスは、ユーザ情報を管理するクラスだと思ってください。Dataアノテーションを使うことで、煩わしいgetterとsetterを省略することができます。めちゃんこ便利ですね。もっと驚いたのは、Spring JPAによってこのクラスの構成と同じテーブルが自動的にDBに生成されることです。また、このクラスをログイン処理に使用するためにSpring Securityで提供されているUserDetailsインターフェースを実装しています。
package com.example.demo.domain.entitiy; import lombok.Data; import org.springframework.security.core.GrantedAuthority; import org.springframework.security.core.userdetails.UserDetails; import javax.persistence.*; import java.util.Collection; import java.util.Date; @Entity @Data public class Employee implements UserDetails { @Id @GeneratedValue(strategy = GenerationType.IDENTITY) private Long Id; private String loginId; private String passWord; private String name; private int age; private String department; private Date createdAt; private Date updatedAt; @Override public Collection<? extends GrantedAuthority> getAuthorities() { return null; } @Override public String getPassword() { return this.passWord; } @Override public String getUsername() { return this.loginId; } @Override public boolean isAccountNonExpired() { return true; } @Override public boolean isAccountNonLocked() { return true; } @Override public boolean isCredentialsNonExpired() { return true; } @Override public boolean isEnabled() { return true; } }
EmployeeRepositoryクラス
Employeeクラスに対応するRepositoryです。今回は、loginIdを使用してログインを行うため、findByLoginId()を追加しています。
package com.example.demo.domain.repository; import com.example.demo.domain.entitiy.Employee; import org.springframework.data.jpa.repository.JpaRepository; public interface EmployeeRepository extends JpaRepository<Employee, String> { public Employee findByLoginId(String loginId); }
LoginServiceクラス
Login処理を行うServiceクラスです。UserDetailsSeviceクラスを実装しています。UserDetailsServiceクラスはSpring Securityで提供されているクラスであり、loadUserByUsernameメソッドを実装することでログインに使用するユーザ情報を検索します。今回は、EmployeeクラスのloginIdを用いてログインを行うため、loadUserByUsernameメソッドの中でemployeeRepository.findByLoginId(username)を実行しています。このメソッドの返り値はUserDetailsインターフェースをのため、ログインに使用したいEntitiyクラスはUserDetailsインターフェースを実装している必要があります。
package com.example.demo.domain.service; import com.example.demo.domain.repository.EmployeeRepository; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.security.core.userdetails.UserDetails; import org.springframework.security.core.userdetails.UserDetailsService; import org.springframework.security.core.userdetails.UsernameNotFoundException; import org.springframework.stereotype.Service; @Service public class LoginService implements UserDetailsService { @Autowired EmployeeRepository employeeRepository; @Override public UserDetails loadUserByUsername(String username) throws UsernameNotFoundException{ Employee employee = employeeRepository.findByLoginId(username); if (employee == null) {throw new UsernameNotFoundException(username); } return employee; } }
WebSecurityConfigクラス
WebSecurityConfigurerAdapterクラスを継承しています。configure(HttpSecurity http)メソッドにより認証が必要なページと不必要なページを切り分けることができます。また、ログインに使用するページ、ログイン成功時に遷移するページ、ログアウト時の処理なども記述することができます。そして、loginProcessingUrlに指定したパスにリクエストが送られるとconfigure(AuthenticationManagerBuilder auth)メソッドが実行され、指定したUserDetailsServiceによりユーザ認証が行われます。
package com.example.demo.config; import com.example.demo.domain.service.LoginService; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.security.config.annotation.authentication.builders.AuthenticationManagerBuilder; import org.springframework.security.config.annotation.web.builders.HttpSecurity; import org.springframework.security.config.annotation.web.configuration.EnableWebSecurity; import org.springframework.security.config.annotation.web.configuration.WebSecurityConfigurerAdapter; import org.springframework.security.crypto.bcrypt.BCryptPasswordEncoder; import org.springframework.security.crypto.password.PasswordEncoder; @Configuration @EnableWebSecurity public class WebSecurityConfig extends WebSecurityConfigurerAdapter { @Autowired LoginService loginService; /** * パスワードをハッシュ化するため * @return */ @Bean public PasswordEncoder passwordEncoder() { BCryptPasswordEncoder bCryptPasswordEncoder = new BCryptPasswordEncoder(); return bCryptPasswordEncoder; } @Override public void configure(HttpSecurity http) throws Exception{ // ログインページ以外は認証が必要 http.authorizeRequests() .anyRequest().authenticated() .and() .formLogin() .loginPage("/login") //ログインに使用するページ .loginProcessingUrl("/login") //ログイン処理を開始するURL .usernameParameter("loginId") //ログイン処理に使用するパラメータ .passwordParameter("passWord") //ログイン処理に使用するパラメータ .defaultSuccessUrl("/emp") // ログイン成功時に遷移するURL .failureUrl("/login?error") //ログイン失敗時に遷移するURL .permitAll(); } @Autowired public void configure(AuthenticationManagerBuilder auth) throws Exception { auth.userDetailsService(loginService).passwordEncoder(passwordEncoder()); } }
デモ
実際にログインをしてみます。LoginID 1000、パスワード 12345の従業員をあらかじめ作成しておきました。
ログイン成功時
ログイン失敗時
WebSecurityConfigクラスで記述した通り、ログインに成功すると/empに遷移し、失敗すると/login?errorとなっていることがわかります。
まとめ
Spring Securityの方でインターフェースが用意されているので、それらを実装するだけでログイン処理を作成することができるのはとても便利だと思います。仕事ではSpring Frameworkを使うことになるのでこれからは積極的にSprinig Bootで開発していけたらと思います。また、TERASOLUNAをオススメされているのでそっちの方も勉強していきたいです。ではでは。
参考にしたサイト
WebSocketでビンゴ!!
こんちか!!たくみんです!!SLP KBIT 2019 アドベントカレンダーの7日目の記事です。
今年もあと3週間ほどになり、各企業では忘年会が行われることではないでしょうか。よく忘年会で行われるのが景品をかけた抽選会やビンゴ大会です。これらの準備は忘年会の幹事や余興担当者が行うことになりますが、大抵は若者がやる羽目になるのではないでしょうか。ビンゴ大会だったら100均でビンゴカードを買ったり、抽選会だったら抽選カードを自作して、忘年会参加者に配布したり、会社の経費で落とすのであれば書類を書いたり...かなり手間がかかるし仕事との両立も難しいと思います。私もおそらく来年に幹事をすることになるため、どうにか楽をできないかと考えていました。そこで、エンジニアらしくITで楽をしようと思い、Web上で動くビンゴゲームのプロトタイプを作ってみました。
目次
方針
ビンゴ大会をWeb上でする場合は、ビンゴで出てきた値がリアルタイムでみんなのビンゴカードに反映される必要があります。そこで、リアルタイムの双方向通信を実現できるWebSocketを用いてビンゴゲームを作りたいと思います。イメージ的には以下のような感じです。

WebSocket
WebSocketサーバ
ビンゴガラガラ画面(主催者用)
送信ボタンを押下すると、WebSocketで1〜25の数字が送信されます。このビンゴは1〜25の数字しかありません。しかも、何回も同じ数字が出ます。普通のビンゴではブーイングの嵐ですが、プロトタイプなのでこれでいいのです。
<html> <head> <title>BingoGaraGara!</title> <script type="text/javascript" src="./bingoGaraGara.js"></script> </head> <body> <h1 id="GaraGararesult"></h1> <button type="button" id="button1">送信</button> </body> </html>
const connection = new WebSocket("ws:localhost:8000"); window.onload = () =>{ let button = document.getElementById("sendButton"); button.addEventListener("click", () => { let GaraGara = Math.floor(Math.random() * 25 + 1); connection.send(GaraGara); result = document.getElementById("GaraGararesult"); result.textContent = GaraGara; }); }
ビンゴカード画面(参加者用)
このビンゴカードは、1〜25が規則正しく並んだものしか作成されません。流石にプロトタイプといえどランダムしないといけないかなと思ったのですが、時間が足りませんでした。処理の流れは以下のようなものになります。
- 2次元配列を元にビンゴカードを作成
- WebSocketで数字を受け取ると、その数字をXに変更(ビンゴカードを開くイメージ)
- ビンゴになっているか判定し、ビンゴになっているとBINGO!と表示
<html> <head> <title>BingoTable!</title> <link rel="stylesheet" type="text/css" href="style.css"> <script type="text/javascript" src="./bingoTable.js"></script> </head> <body> <h1 id="result"></h1> <table border="1" class="bingo" id="bingo-table"></table> </body> </html>
let bingo = [["1","2","3","4","5"],["6","7","8","9","10"],["11","12","X","14","15"],["16","17","18","19","20"],["21","22","23","24","25"]]; // ビンゴボード作成 let createBingoTable = () => { let bingoTable = document.getElementById("bingo-table"); for (i = 0; i < bingo.length; i++) { tr = document.createElement('tr'); tr.className = "bingo-tr"; for (j = 0; j < bingo[i].length; j++) { td = document.createElement('td'); td.textContent = bingo[i][j]; td.className = "bingo-td"; td.id = "bingo-td-" + (i * 5 + j + 1); tr.appendChild(td); } bingoTable.appendChild(tr); } } // ビンゴボード更新 let updateBingoTable = (value) => { for (i = 0; i < bingo.length; i++) { for (j = 0; j < bingo[i].length; j++) { if (bingo[i][j] === value) { let bingoTd = document.getElementById("bingo-td-" + (i * 5 + j + 1)); bingoTd.textContent = "X"; bingo[i][j] = "X"; } } } } // ビンゴ判定 let checkBingo = () => { if (checkBingoCell(0,0,1,0)) {return true;} if (checkBingoCell(0,1,1,0)) {return true;} if (checkBingoCell(0,2,1,0)) {return true;} if (checkBingoCell(0,3,1,0)) {return true;} if (checkBingoCell(0,4,1,0)) {return true;} if (checkBingoCell(0,0,0,1)) {return true;} if (checkBingoCell(1,0,0,1)) {return true;} if (checkBingoCell(2,0,0,1)) {return true;} if (checkBingoCell(3,0,0,1)) {return true;} if (checkBingoCell(4,0,0,1)) {return true;} if (checkBingoCell(0,0,1,1)) {return true;} if (checkBingoCell(4,0,-1,1)) {return true;} return false; } let checkBingoCell = (startX, startY, dx, dy) => { count = 0; i = startY; j = startX; while(true) { if (i >= 5 || j >= 5) { break;} if (bingo[i][j] !== "X") {break;} count++; i += dy; j += dx; } if (count == 5) { return true;} return false; } window.onload = () => { createBingoTable(); connection = new WebSocket("ws:localhost:8000"); connection.onopen = function(e) {console.log("connected")} // メッセージを受け取ると該当するボードが開く connection.onmessage = function(e) { console.log(e.data); updateBingoTable(e.data); if(checkBingo()) { result = document.getElementById("result"); result.textContent = "BINGO"; } } }
デモ

おわりに
プロトタイプということでまだまだ未完成で考慮すべき点が色々あります。完全版にするためには以下のような点を考慮しないといけないのかなと思います。
- 技術選定
- そもそものシステム構成
- Developer Toolでのビンゴカード書き換えの対策
- ビンゴカードのランダム化
- ビンゴ部屋的なやつ
- 参加人数やリーチの人数、ビンゴの人数のリアルタイム表示
- スマホでの使用を前提としたUI
今はただのJSのみを使用していますが、Reactとか使うのか、Railsといったフレームワークを使うのかなど色々決めないといけないなと思います。 そもそも、急ピッチで作ったため、WebSocketの理解が浅くまだまだわからない点が多いです。このビンゴゲーム作成を通してWebSocketについて理解できたらなと思います。そして、来年の忘年会までに完全版を作成し、ドヤ顔をしたいです。ではでは。
参考にしたサイト
Ansibleで環境構築をしてみた(Ubuntu 18.04)
こんちか!!たくみんです。今回はAnsibleを使って、Vagrantを用いて作成した仮想環境(Ubuntu 18.04)の簡単な環境構築を行ってみたので記事にしたいと思います! 本来は、冪等性を確保するためにインストールはaptではなくソースビルドを行ったりするみたいなんですけど、 今回は初めてという事で普通にaptでインストールを行っていきます。

目次
Version
今回使用するVersionは次の通りです。
- Python : 2.7.10
- Ansible : 2.8.4
- Vagrant : 2.2.2
- VirtualBox: 6.0.2 r128162 (Qt5.6.3)
自動化するタスク
Ansibleを使って、自動化するタスクは以下のものになります。
Vagrantfile
Vagrantfileは以下のような感じです。
Vagrant.configure(2) do |config| config.vm.define "target" do |node| node.vm.box = "bento/ubuntu-18.04" node.vm.hostname = "target" node.vm.network :private_network, ip: "192.168.100.20" node.vm.network :forwarded_port, id: "ssh", guest: 22, host: 2220 end end
Playbook
Playbookのディレクトリ構成
Playbookのディレクトリ構成はこんな感じです。
├── hosts // Playbookを適応させる対象を決めるやつ ├── roles │ ├── apt // apt installをやるやつ │ │ └── tasks │ │ └── main.yml │ ├── dotfile // dotfileをgit cloneして設定するやつ │ │ └── tasks │ │ └── main.yml │ ├── ruby // rbenvインストールするやつ │ │ └── tasks │ │ └── main.yml │ └── zsh // zshを設定するやつ │ └── tasks │ └── main.yml └── site.yml // Playbookの本体
hosts
hostsファイルは以下のような感じです。Vagrantで作成した仮想環境を対象にします。
[target] 192.168.100.20
site.yml
site.ymlは以下のような感じです。それぞれ別ファイルに分けたタスクを 順次実行しています。
- hosts: all # hostsファイルにある全てが対象 user: vagrant # userはvagrant become: yes # sudoを使う roles: - apt - dotfile - zsh - ruby
aptのmain.yml
aptディレクトリのmain.ymlは以下のような感じです。結構インストールしていますが、だいたいrbenvとruby-buildに必要なやつです。
- name: apt install apt: name: - zsh - git - gcc - emacs - autoconf - bison - build-essential - libssl-dev - libyaml-dev - libreadline6-dev - zlib1g-dev - libncurses5-dev - libffi-dev - libgdbm5 - libgdbm-dev - cmake update_cache: yes # インストールする前に apt-get updateを実行 force_apt_get: yes # apt-getを使う
zshディレクトリのmain.yml
タスクとしては、以下のような感じです。
Ansibleのshellモジュールとcommandモジュールは自動で冪等性を確保してくれないため、 現在のシェルがzshかどうかで処理を分ける事で冪等性を確保しています。
これをPlaybookにすると以下のようにになります。
- name: zsh check # 現在のシェルがzshかどうかチェック become: no # sudoでやるとvagrantユーザのシェルをみてくれないためoff shell: echo $SHELL register: current_shell # shellで実行した結果をcurrent_shellに格納 changed_when: no # 毎回changedになってしまうのでoff - name: zsh set # 現在のシェルがzshじゃなければzshに変更 shell: chsh -s '/usr/bin/zsh' vagrant when: "'zsh' not in current_shell.stdout"
dotfileディレクトリのmain.yml
タスクとしては、以下のような感じです。
これをPlaybookにすると以下のようにになります。
- name: git clone dotfile become: no # sudoをつけるとvagrantユーザのHOMEディレクトリに置いてくれない git: repo: https://github.com/takuminish/.dotfiles dest: ~/.dotfiles - name: zsh symlink become: no file: src: ~/.dotfiles/zsh/{{ item }} dest: ~/{{ item }} state: link # シンボリックリンク force: yes # ファイルがあったら置き換える with_items: - .zsh.d - .zshrc - name: emacs symlink become: no file: src: ~/.dotfiles/emacs/{{ item }} dest: ~/{{ item }} state: link force: yes with_items: - .emacs.d
rubyディレクトリのmain.yml
タスクとしては、以下のような感じです。本当はrbenvを使ってRubyのインストールまで行っても良かったんですが、そこまでする必要はないのかなと思ったのでタスクからは省きました。
- rbenvをgit clone
- ruby-buildをgit clone
これをPlaybookにすると以下のようにになります。
- name: git clone rbenv become: no git: repo: https://github.com/rbenv/rbenv dest: ~/.rbenv - name: git clone ruby-build become: no git: repo: https://github.com/rbenv/ruby-build dest: ~/.rbenv/plugins/ruby-build
実際にやってみた
上記のPlaybookを実際に実行してみました。
vagrant up
vagrant upで仮想環境を起動します。
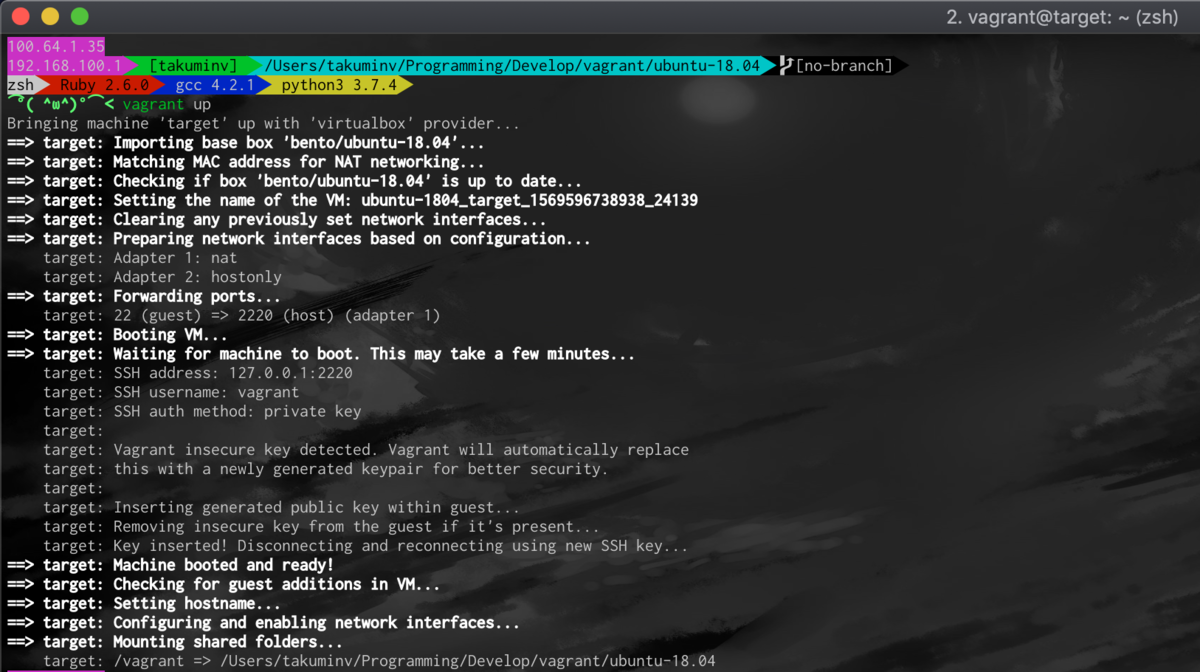
vagrant ssh
vagrant sshで仮想環境にリモートログインしてみます。
なんて貧相なターミナルなんでしょう。
ssh-copy-id
Ansibleを対象に適応させるには、対象に公開鍵認証でSSHを行えるようにする必要があります。そのため、ホストの公開鍵をAnsibleの対象に渡しておきます。
ansible-playbook
では、Ansibleを実行します。このWARNINGはなんなんですかね。調べてもよくわからなったので知っている方がいたら教えて欲しいです。
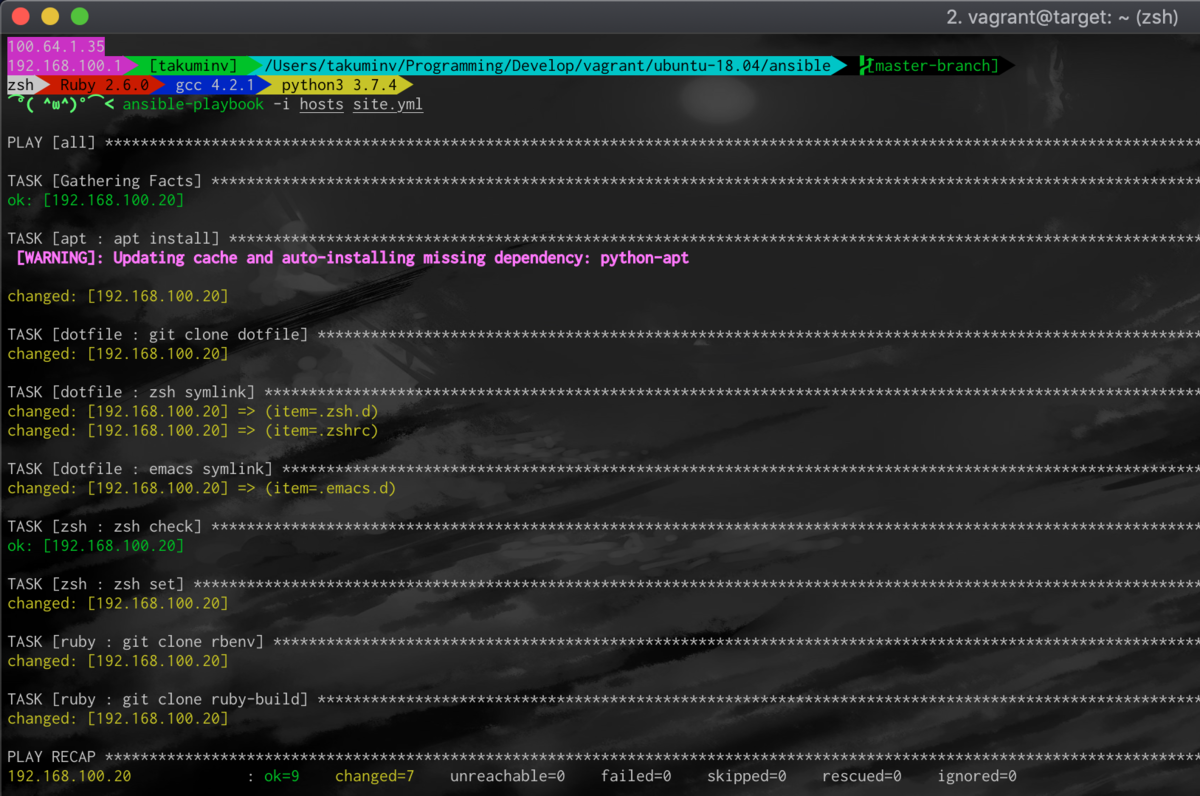
実際にSSHでログインして、しっかり環境構築ができているのか確かめてみましょう。
ちゃんとターミナルが私の作成したものに変わっています!
終わりに
Ansibleは学生の頃にちょびっと触っただけだったんですけど、なんとか環境構築ができて良かったです。今はUbuntuの環境構築のみですが今後はCentOSだったりMacの環境構築もできたらと考えています。ではでは。
参考にしたサイト
CIのテスト結果は黒澤ダイヤちゃんに言われたい
はじめに
こんちか!!たくみんです。久しぶりに記事を書きますが、今回はSlackBot(厳密にはBotではない)です。そろそろ僕もCircleCIとか使って、開発して自動でテストが走って、また開発してといういい感じの奴がしてみたいと思っていました。そこで、CircleCIについて調べているとテストの結果をSlackに通知してくれる奴(Chat Notifications)があるみたいなので、早速自分のSlackに導入してみました。

なんやこのおもんない通知は!
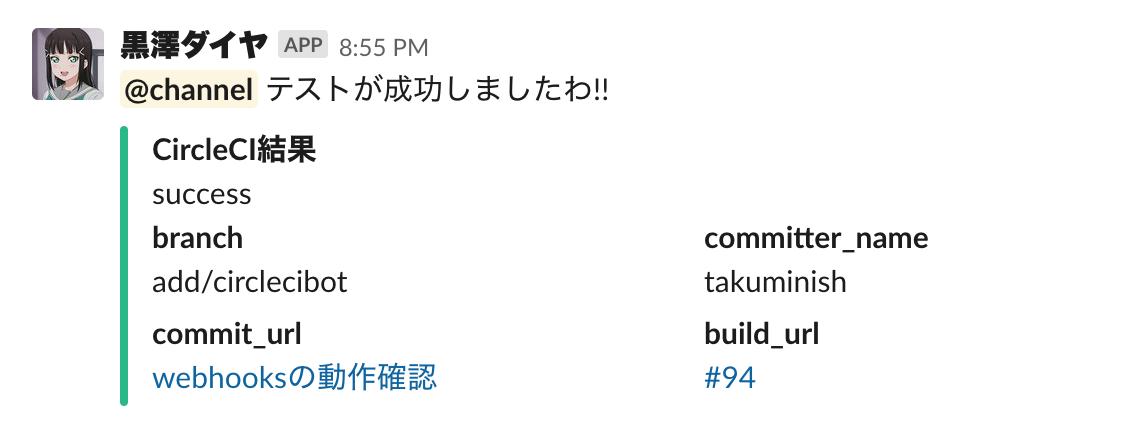
というわけで、自作で作ってみました。それが黒澤ダイヤBOTです。

各種バージョンと動作環境
このBotはSinatraを使用しており、動作環境としてPaasのherokuを使用しました。
Slackに通知する情報
テスト結果の情報として表示するのは以下の5つです。
- テスト結果
- ブランチ名
- コミットしたユーザ
- GitHubのコミットページのURL
- CircleCIのジョブページのURL
ソースコード
やってることはとても単純で、CircleCIから送られてきたJSONデータから、上記の5つの情報を抜き取り、SlackにPOSTしているだけです。
Sinatraを動作させるapp.rbとSlackに通知する情報を管理するpayload.rb(Payloadクラス)の2つを作成しました。
app.rb
require 'sinatra' require 'json' require 'dotenv' require './payload.rb' Dotenv.load get '/' do end post '/' do params = JSON.parse request.body.read # 受け取ったJSONデータを格納 # JSONデータから必要な情報のみを取得 payload = Payload.new(params['payload']['reponame'], params['payload']['outcome'], params['payload']['branch'], params['payload']['committer_name'], params['payload']['subject'], params['payload']['all_commit_details'][0]['commit_url'], params['payload']['build_url'], params['payload']['build_num'], ENV["WEBHOOKURL"]) payload.post # SlackにPOST end
payload.rb
require 'net/http' require 'uri' class Payload # コンストラクタ def initialize(reponame, outcome, branch, commiter_name, commit_message, commit_url, build_url, build_num, webhook_url) @reponame = reponame @outcome = outcome @branch = branch @commiter_name = commiter_name @commit_message = commit_message @commit_url = commit_url @build_url = build_url @build_num = build_num @webhook_uri = URI.parse(webhook_url) # CI結果によって、通知するコメントと、Payloadの色を変更 @color = "good" @pretext = "テストが成功しましたわ!!" if @outcome === "failed" @color = "danger" @pretext = "テストを失敗するなんてブッブーですわ!!" end end def post @post_data = { attachments: [ { title: "#{@title} CircleCI結果", pretext: "<!channel> #{@pretext}", text: @outcome, fields: [ { title: "branch", value: @branch, short: "true" }, { title: "committer_name", value: @commiter_name, short: "true" }, { title: "commit_url", value: "<#{@commit_url} | #{@commit_message} >", short: "true" }, { title: "build_url", value: "<#{@build_url} | ##{@build_num} >", short: "true" } ], color: @color } ] } self.log # log出力 Net::HTTP.post_form(@webhook_uri, {payload: @post_data.to_json}) # SlackにPOST end def log puts "reponame: #{@reponame}" puts "outcome: #{@outcome}" puts "branch: #{@branch}" puts "commiter_name: #{@commiter_name}" puts "commit_message: #{@commit_message}" puts "commit_url: #{@commit_url}" puts "build_url: #{@build_url}" puts "webhook_uri: #{@webhook_uri}" puts @post_data end end
Githubのページ
おわりに
CircleCIから送られてくるJSONデータの構造を理解するのにとても手間取り、3日くらい作業がストップしてしまいました。最終的にpryで確認すれば良いことに気づいてなんとかBotを作ることができました。この表示が見やすいかどうかは人それぞれですが、僕は満足です。
参考ページ
SECCON Beginners CTF 2019 WriteUp
はじめに
こんちか!たくみんです。2019年05月25日 15:00から26日 15:00まで行われたSECCON Beginners CTFに友人と2人で参加しました。
結果は以下の通りで、666チーム中150位でした。

今回僕が解くことができたのは、以下の2問なのですがMisc Welcomeは解説してもしょうがないので、WebのkatsudonだけWriteUpしていきます。
- Web katsudon
- Misc Welcome
Web katsudon
問題文
Rails 5.2.1で作られたサイトです。
https://katsudon.quals.beginners.seccon.jp
クーポンコードを復号するコードは以下の通りですが、まだ実装されてないようです。
フラグは以下にあります。 https://katsudon.quals.beginners.seccon.jp/flag
# app/controllers/coupon_controller.rb class CouponController < ApplicationController def index end def show serial_code = params[:serial_code] @coupon_id = Rails.application.message_verifier(:coupon).verify(serial_code) end end
解法
とりあえず、https://katsudon.quals.beginners.seccon.jp/flagにアクセスすると以下のようなページに飛ぶ。
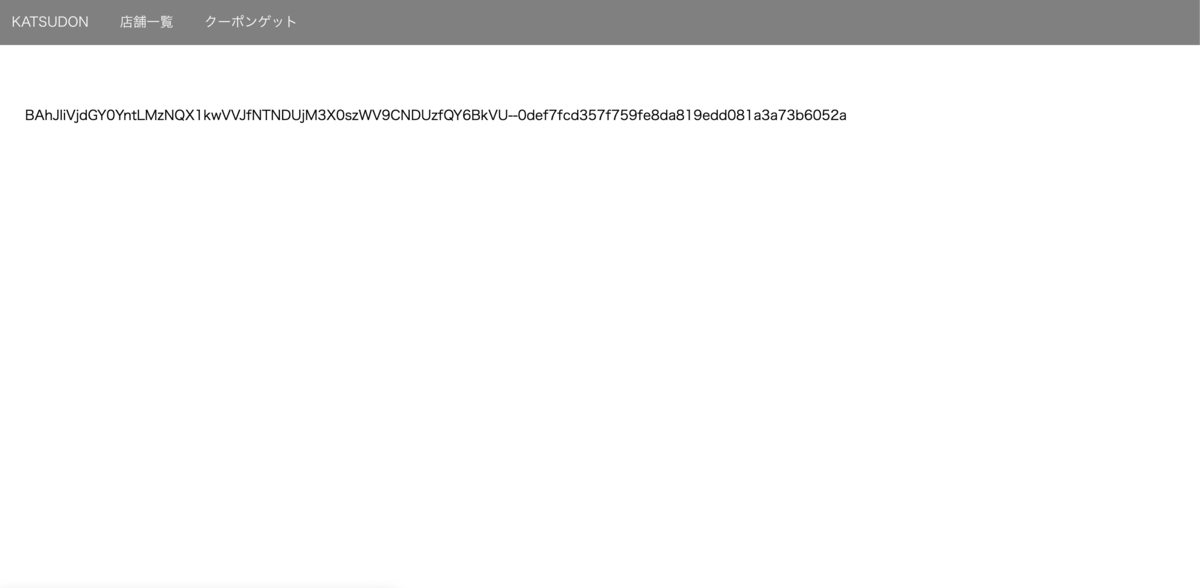
ここに表示されているコード(クーポンコード)を復号するとフラグ(シリアルコード)がゲットできると思うため、どのように暗号化されているかを調べる。 暗号化に関わってくるのは、問題文中の以下のコードである。
@coupon_id = Rails.application.message_verifier(:coupon).verify(serial_code)
message_verifierについて調べると以下のQiitaの記事が見つかった。
この記事には、
Rubyオブジェクトを文字列化しBase64エンコードした文字列と、Base64エンコードしたものを鍵と組み合わせてSHA1でハッシュ化した文字列を--で繋げます。
と書かれているため、暗号化されたコードの最初から、--までの文字列をBase64で復号すれば、フラグがゲットできる事になる。
よって以下のように、暗号化されたコードのうち、--までのBAhJIiVjdGY0YntLMzNQX1kwVVJfNTNDUjM3X0szWV9CNDUzfQY6BkVUをBase64で復号することでフラグゲット!!
$ echo "BAhJIiVjdGY0YntLMzNQX1kwVVJfNTNDUjM3X0szWV9CNDUzfQY6BkVU" | base64 -D
I"%ctf4b{K33P_Y0UR_53CR37_K3Y_B453}:ET%
おわりに
ほとんど足を引っ張ったまま終わってしまったなという印象でした。来年にはWebの問題をもっと解けるようになりたいなと思ったので、他の人のWriteUp等を参考にしながら勉強しようかなと思います。ではでは。